Matrix, GOP and the remainder of the world
of Kika
Before the Encoden of a video in MPEG1 or MPEG2 the same questions arise again and again: What do I take now? A long GOP? Or nevertheless better a short? And which is the best matrix? Is usable also for all kinds of film? And why do I make that at all? Questions over questions, fortunately gibt's answers, even if these are perhaps nevertheless not necessarily the answers, which expected many.
Thus, my contribution in EDP-tap here is divided into four sections:
DCT & matrix, which is that?
Motion prediction and Estimation
GOP sizes and which happens thereby
Practice: As one converts the knowledge from the three first parts into genuine results
We begin now directly times with the first contribution:
Block, DCT and matrix or "of stones and waves in the lake"
OK ONE, in order to understand, how with the matrix and the GOP lengths like that is, one must only times the bases. We make the beginning with block, the DCT and the matrix.
First one must know that the smallest picture unit existing in MPEG is not a pixel, but a block of 8x8 of pixel. I use a highly simplified model, that for the explanation now times to the address of the professionals, who perhaps turn in view of some the following something "indistinct" explanation the nose.
At the block the so-called DCT (Discrete Cosinus transformation) one accomplishes. A procedure, with which the block is divided into its frequency components.
Which develops thereby and is stored in place of the original pixels, is a matrix from frequency interference , whereby each individual cell the frequency spectrum of the entire original 8x8-Block represented (for the sake of simplicity I proceed times from a S/W picture and not with a farbbild).
However only very limited, because the first cell applies (more exactly said: the first element) alone can show quasi only a simple grey surface and stands thus for the average brightness of the entire block. Ascending vertical "bars" are then added to the right, so that the respected cell contains a sample from lattice bars.
Similarly to it it behaves with the lines. From above downward ever more horizontal bars are added, at the end develop thereby a streifenmuster. Diagonally that has the effect that a ever more complex gittermuster develops. The 64ste cell finally is from the dissolution of frequency able to show the picture without each quality loss.
How the whole looks, one can infer from the picture.
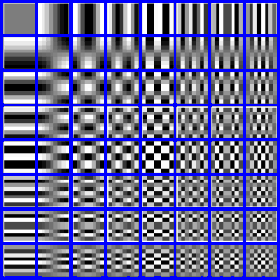
Who believes now to have to store only contents of the last cell which errs, even if that contradicts now apparently, which I wrote so far. It is however easy to understand if one recalls oneself in the memory that only interference samples are stored, only several of it results in something that could really call itself picture.
To explain, very extensive mathematics knowledge presuppose that now more near, which I do not have also, left wir's thus with it: A good mathematician could compute theoretically from the wave interference (element of the block matrix after the DCT) on a lake (the block), like many stones (pixels) where in the water were thrown (Postion of the pixel) and those were as heavy (the brightness), and in the same way later also again the picture are produced. The stone analogy is important, because we still need it later.
Important thereby however still one is: The cells with higher cell numbers take up more complex spectra. If one omits now columns, lines or also cells, in order to save storage location, then one takes step for step at complexity to the original picture. That can be done up to a certain point completely well, because the human eye cannot see so good eh.
So, we divided the picture into block to 8x8 pixels and those to have we to frequencies converted. Beautifully complicated, however not yet only one byte brings space saving. Those comes only in the next step, quantization, for which the matrix liked all-side is used (which always).
The DCT naturally right-of-comma positions are completely loss-free from the basic principle, thus that in the cells however only integer values are stored, are lost, and by setting the range of values on 8, 9 or 10 bits likewise error, often mentioned, develops for quantization errors which is wrong (correctly rather DCT error, but rounding error would be trifft's perfect), because we still at all did not quantize.
We make that now with the matrix?
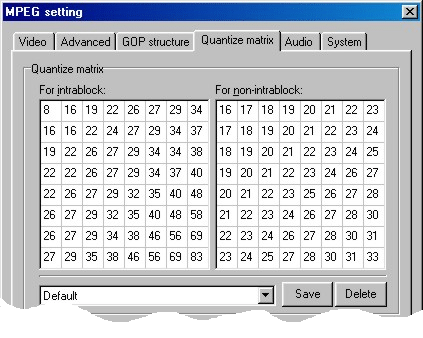
Most readers will have noticed the above picture already times in TMPGEnc; -)
The task of such a matrix is it to homogenize cell contents if possible thus each other adapts (as this new film is called? "which does not fit, made suitable?". I think, meet the procedures completely well).
This adapting is important together, since in the following step a compression method is used (RLE), which is dependent on the fact that as much as possible same values follow one behind the other.
As we know now, at present cell contents (elements) stand representatively of the complexity of the block. The quantization matrix contains numbers, which are charged with those of cell contents. The trick is now that to select the numbers of the matrix in such a way that the desired goal is achieved of bringing i.e. as much as possible cells on same values. Correctly! The goal is not necessarily to set as much as possible cells to zero although one can also make.
Which we reach with the fact are that the RLE coding seizes now better. It checks simply whether several same values follow one behind the other. It stands at the end of quantization e.g. in four cells successively (which are that are dependent on the Scanorder, which sequence, in which the cells are queried) same values, we assume times, that is the 8, then no more are only stored four respecting, but the value and the found number. Thus instead of 8,8,8,8 only 4,8. One can save much place with. That is the positive effect of quantization.
Naturally the thing has also a hook: We change thereby also the original frequency information, which becomes "weakened" quasi - and leaves itself starting from a certain degree of quantization, i.e. then, if from it too many rounding errors result, cancel no longer!
The more brutally with it a matrix proceeds, the better (there are exceptions, therefore e.g. the CG matrix exists) in addition, can be compressed, the more frequency portions and concomitantly restorable picture information is lost irreparably. And we do not want that.
", but high frequencies, that is nevertheless noise, and that become also equivalent loose we thereby ". Was it that, which many wanted to now object? Yes? I must disappoint you, am correct only partially.
Reminds you: Interference sample provides the DCT! For each cell based on the entire block and evenly not only on a frequency or a certain frequency band. And already not at all related to any special pixel within the block. High quantizing far away thus the noise really, but does not take to the picture at complexity. Thus is that noise perhaps no longer completely so strongly afterwards visibly, it is however still available!
OK ONE, after we versaut now the picture so strongly, one asks nevertheless intended, how one wins from it then nevertheless again a good picture, and for it needs I the stones, the mathematician and the lake of even.
The mathematician tries to calculate by the wave samples (cell contents), which it sees, what for stones (our pixels, which we want to again-have sometime) where in the water (position of the pixels) were thrown. In addition however only the data of two are necessary, the values third result inevitably from those both first with three stones. In the plain language: It calculates 2 stone post office ions and other data, sees however that there still waves are from a third stone. From the past data and what one has there otherwise still, can be derived, which when and where to it led. Nothing different one does later the reversal of the DCT, which iDCT. Each cell of the block is thus one of our stones (pixels), and/or. the information about such with reference name on all different. In the plain language: Each cell is one of the waves and/or the interference sample of several, which one of the stones produced with the impact on the water.
First with the help of the matrix hopefully stored in the MPEG Stream (it is not stored, the standard matrix is used, was however with the Encoden another active, develops then for garbage) the quantization effect turned around, which would be by the way loss-free, would give it not a small problem: During quantization rounding error results and from it also unintentional zero values, and the more, the more strongly a matrix quantized.
In order to explain, I use now times addition and subtraction, although that is mathematically absolutely wrong. I want to only show thereby, what quantization errors are at all and how it to affect itself. We accept thus times, the original cell values after the DCT (the ausschnittsweise) following were: 24, 16, 22, 23, 22, 11, those is now quantized (as said, we subtracts simply times) with the corresponding matrix values 22, 22, 22, 24, 24, 24. At the end comes thus thereby out (negative values and such with decimal places gibt's thereby not): 2, 0, 0, 0, 0, 0. Now we turn quantization with the same matrix: 24, 22, 22, 24, 24, 24, and which does not have much with the original picture any longer to do (read yourself however prima to compress: "Hurra! No block building with fast movements in my video more, super a matrix ", so sprach's the user. Whereupon Kika yawned and meant laconic: "is correct, and the picture is also so marvelously indistinct! And only pumping! Ingeniously! As the artist is called?") Note of the author: Did someone understand the joke?
OK ONE, OK ONE, in reality are simply added and are not subtracted, in addition only also not in each case cell contents enter also back computation to pixels; all white I also (always these interruptions, terribly * grins *), it shows however, what happens, if (too) highly and why then evenly no reasonable picture is quantized more be produced can.
Thus, now we know thus, like the smallest picture unit with MPEG, i.e. the block, and in addition the DCT and quantization (and thus the matrix) functions, at least roughly. From this then the question arises: What should do a good matrix?
Oh, one am still guilty I to you: the explanation of the term "Scanorder".
One proceeds from the theory that after the DCT and quantization two neighbouring elements exhibit same values. Neighbouring one must see here however two-dimensional. With it values next to one another are meant within a line or a column, but within a certain frequency spectrum, therefore when querying cell contents in the zigzag sample one proceeds, which the Scanorder concerned the nice name ZigZag brought in.
With Interlaced video one uses the so-called Alternate Scan. Also it proceeds after a zigzag sample, although one, which looks rather chaotic at first sight. It carries however with on Fields and not on Frames which is based video format calculation for the screen layout.
One sees the two possibilities completely good in the picture.
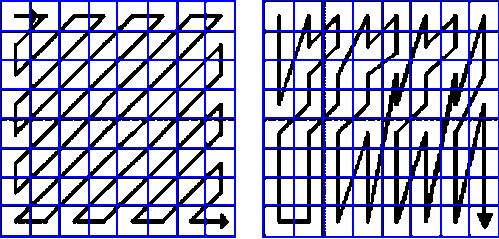
On the left of the ZigZag -, on the right of the Alternate Scan
OK, according to so much theory now little practice. We all want to store our films as space-saving as possible and in as high a quality as possible.
In the quality we can change hardly something, because all the same which we to do, thus all the same which matrix we to use, after quantization can the picture never again be, which it was in the original. It becomes always somewhat more indistinct and also pale. Which we can do however, verb luring is minimize at the compression screw to turn and.
In addition the still following: From so far the saying it can be derived that the original picture can be still reconstructed also then, if at the disposal is to fewer information thus complete frequency ranges is removed. The throw more information away we thus with quantization, can the better be compressed. We pay with a loss at image definition and color brilliance.
A quantization matrix is nothing different one than a filter for frequency ranges, and that know we all from the audio range. With music CDs the maximum audiofrequency is 22 kHz, which do not know human ear however at all so high frequencies or only very badly to notice, one makes oneself for what during the audio compression, and frequencies over 16 kHz simply cuts off. Exactly we can reach that also with the matrix during the MPEG compression.
A matrix consists of 8x8 fields. From on the left of to the right their element ever more highly becoming line frequencies stand, from above downward for the field frequencies.
A low-pass filter, thus one, which lets low frequencies through, high however cuts off, would see as matrix so out (the red marked fields are the changed fields. Basis was the standard attitude of TMPGEnc 2.53.35.130):

Abb: 1 (by S.U)
With this matrix the high frequency portions are completely thrown away.
To it a high-pass filter would look similar thus as follows:

Abb: 2 (by S.U)
Such a filter lets the low frequencies in the Nirwana disappear.
The third kind of filter, which gives it, i.e. the band-pass filter, can be likewise carried out then:

Abb: 3 (by S.U)
It cuts all frequency ranges even, without preferring one. Quite also sense can make, i.e. with pictures, which are not so complex on their part from, for example zeichentrickfilme (did not computer-animate! Under TMPEG we regain in the attitude "CG/Animation").
Now most of you saw surely already times to stencils for high compression, and those look completely differently. Correctly, but there is a stupid reason: The television! Because that has a clearly visible line however no visible column structure. With monitors that is differently, since PCS work now times pixel-oriented, television does that not, and to which one must unfortunately consider.
With the Cinemacraft Encoder (CCE) gives it e.g. a Low bit rate matrix with the following structure ("xx" to show and only that no change was made here):

Abb: 4 (by S.U)
This matrix far away almost exclusively horizontal frequencies and leaves the vertical unaffected. One great thing, because the image quality suffers from it only very very few. That is because of the fact that the television picture has (seen digital) always 576 lines, which horizontal definition is measured however in lines, roughly said in time periods, and depending upon classification of signals the dissolution is horizontal anyway lower.
The CCE offers also the possibility, this matrix of transponieren (rotate), looks then in such a way:

Abb: 5
(by S.U)
Merry idea, because leads, since we have CELEBRATIONS a dissolution of vertical, to line structures in the picture.
That is by the way also the reason, why the low-pass filter functions above with pictures on the PC monitor outstanding (better geht's not!), with videos for the television however is suddenly apparently worse. In addition it agrees only in parts with the Scanorder.
Thus, naturally most know also Angels matrix (glassing:
http://www.unikassel.de/~eckhardm/hq.htm), which sets diagonally values to 99. What makes exact then? We regard it to us in a simple variant once:

Abb: 6 (by S.U)
Tja, from the view of the frequency spectra a rather unfortunate solution, since it goes to spectra in each direction only the half way and only partially far away.
But still times the chart looks at you to the Scanorder, then see you immediately, what here the trick is: Values in exactly the correct order are highly quantized, whereby the RLE compression functions outstanding. Problematic it is even that she removes also field frequencies, which because of the mentioned banded structure of the television picture is not very favorable. Who wants to cheat however with the Scanorder, no other choice has.
The thing becomes nearly optimal, if we combine two stencils: The Low bit rate of CCE and the fishing rod matrix, which in such a way then looks:

Abb: 7
(by S.U)
The line frequencies are cut strong, the vertical a little, and the lower part agrees with the Scanorder.
So, I hope that by these examples became clear now, what stencils for high compression actually do.
Replaces "xx" everywhere by the values of the standard matrix of the Encoder and plays under attention its that was said here, with the arrangement of the 99er values, and already can experiment you, until the CCU smokes.
The trick when the investigation optimization possibilities is now that to find not only the correct arrangement of the values but also according to favorable values. It throws the 99 away the frequencies completely which always provides for Unschaerfe, if one creates it however to set the values in such a way that the frequency portions remain, the RLE compression however nevertheless well seizes, then we have the optimum...
Allerdings research to it already since many years the people, without the solution to have found. And starting from a certain bit rate optimizations make much sense the place saving also not more, then it concerns suddenly to produce as sharp a pictures as possible. And in a matrix thought in addition 99 does not occur with security anywhere

That were now all examples of the Intra matrix, the non Intra I had consciously ignored, because partially different rules apply there. A rule is universal thereby: It should not be as highly quantizing as the Intra matrix.
In addition all stencils with exception of the three filters (low -, volume and high-pass), presented here, are only with progressive videos reasonably applicable, not with Interlaced video.
By the way, that would times be a good idea for programmer von AVISynth- and VirtualDub VirtualDub-Filtern: A freely adjustable Quantisierer! One, which weaken in addition, can strengthen. Which we would have then, would be a Equalizer for pictures and videos, and thus one could do much...
That was however now real it. The next part, which becomes times finished hopefully sometime, turns then around the topic: Motion Prediction and Estimation - ship sinking under less favourable conditions!
Of you,
Kika
P.S. Thank you also on shh, of many surely as programmers of the Tools FitCD admits, which stood for me with the somewhat more complicated parts with advice and act to the side.